| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 마이온컴퍼니
- Python
- DFS
- BFS
- GNN
- 멋재이사자처럼
- TiL
- likelionlikelion
- 인턴10
- paper review
- tog
- 마이온
- 파이썬
- 알고리즘
- seaborn
- SQL
- 프로젝트
- 멋사
- Join
- likelion
- ux·ui디자인
- 멋쟁이사자처럼
- parklab
- intern10
- graphrag
- 그리디
- Rag
- DP
- 시각화
- folium
- Today
- Total
지금은마라톤중
[Paper review] GNN-RAG: Graph Neural Retrieval for Large Language Model Reasoning 본문
[Paper review] GNN-RAG: Graph Neural Retrieval for Large Language Model Reasoning
Ojungii 2025. 2. 3. 11:29GNN-RAG:
Graph Neural Retrieval for Large Language Model Reasoning
0. Abstract
GNN-RAG는 Knowledge Graph Question Answering(KGQA) 문제를 해결하기 위해 GNN(Graph Neural Network)과 LLM(Large Language Model)을 결합한 혁신적인 Retrieval-Augmented Generation(RAG) 프레임워크를 제안합니다. 기존의 텍스트 기반 RAG 접근법이 KG의 복잡한 구조를 효과적으로 처리하지 못하는 한계를 극복하기 위해, 본 연구는 GNN 기반 검색을 통해 관련 정보를 효율적으로 추출하고, 이를 텍스트화하여 LLM의 입력으로 활용합니다. 특히, Retrieval Augmentation(RA) 기법을 통해 GNN과 LLM의 강점을 결합하여 검색 정확도를 향상시키고, 복잡한 질문에서의 성능을 크게 개선하였습니다. 본 연구는 WebQSP와 CWQ 데이터셋에서 최고 성능을 기록하며, GNN-RAG의 효율성과 확장 가능성을 실증적으로 입증합니다.
1. 서론 (Introduction)
문제 정의
- KGQA는 자연어 질문에 답하기 위해 지식 그래프(KG)를 사용합니다. 이는 대규모의 구조적 데이터에서 유용한 정보를 검색하여 질문에 답하는 데 핵심적인 역할
- 기존의 RAG(Retrieval-Augmented Generation)는 텍스트 기반 정보 검색에 초점을 맞추었으나, KG의 복잡한 그래프 구조를 처리하는 데 한계를 보임.

기존 한계
- LLM 기반 검색은 질문을 그래프 탐색 경로로 변환하거나, 관계를 탐색하는 방식으로 작동하지만, 다수의 LLM 호출이 필요하여 비효율적
- GNN 기반 방법은 그래프 구조를 잘 탐색하지만, 텍스트 기반 질문과의 상호작용 능력이 부족하여 단순 질문에서 제한적
논문의 기여
- GNN-RAG: GNN을 활용하여 KG에서 질문 관련 정보를 효율적으로 검색하고, 이를 LLM에 제공하여 최적의 성능을 달성합니다.
- 복잡한 질문(WebQSP와 CWQ 데이터셋)에서 기존 모델 대비 최대 15.5% 성능 향상을 기록하며, 적은 계산 자원으로도 높은 효율성을 자랑합니다.

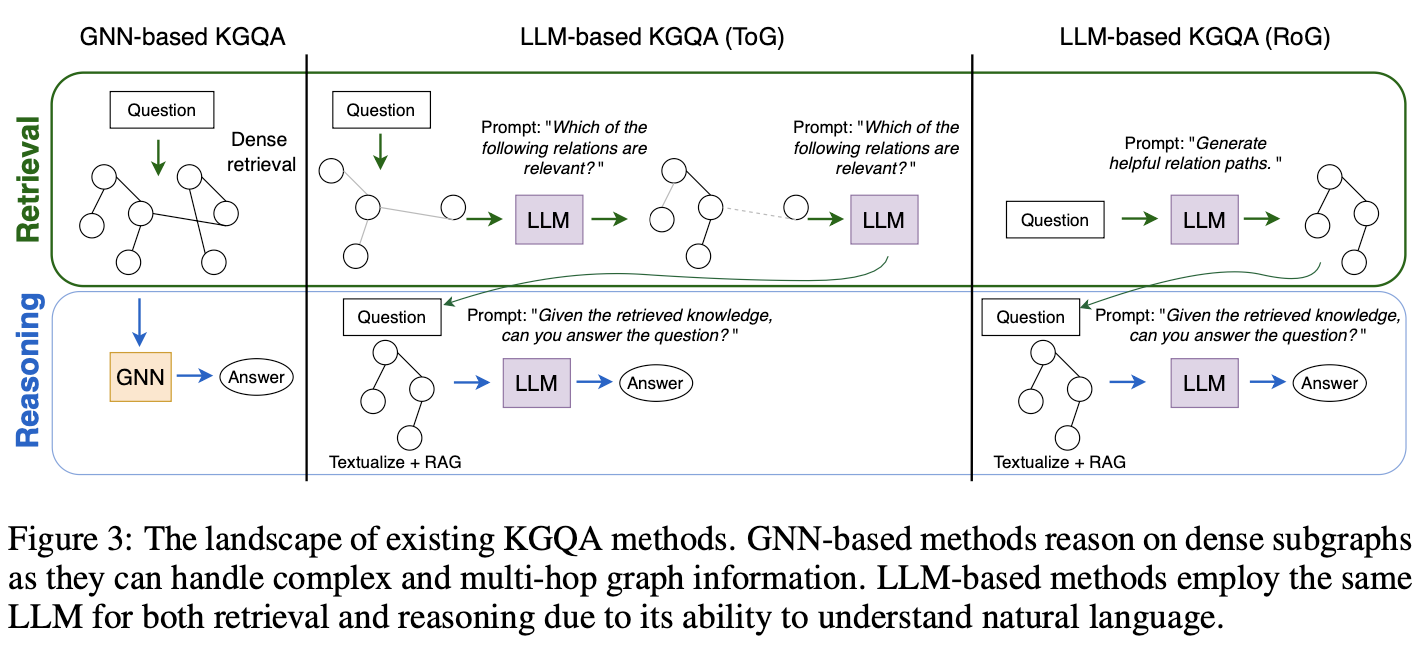
2. 관련 연구 (Related Work)
KGQA 방법 분류
- Semantic Parsing (SP):
- 질문을 SPARQL과 같은 논리적 질의로 변환 후 실행합니다.
- 한계: 논리적 질의 학습 데이터 생성이 어렵고, 변환 과정에서 오류가 발생할 가능성이 높습니다.
- Information Retrieval (IR):
- 약한 지도 학습(weak supervision)을 통해 그래프 하위 구조를 검색합니다.
- GNN-RAG는 IR 방식에 속하며, 구조적 데이터를 효과적으로 처리합니다.
GNN과 LLM 결합
- 기존 연구들은 그래프와 텍스트 간의 모달리티 차이를 해결하는 데 어려움을 겪었습니다.
- GNN-RAG는 GNN과 LLM의 역할을 분리하고 상호작용을 강화하여 이 문제를 해결합니다.
GraphRAG
- 기존 GraphRAG 접근법은 노이즈와 비효율적인 검색으로 인해 성능이 저하되었습니다.
- GNN-RAG는 GNN을 최적화하여 질문과 관련된 정확한 그래프 정보를 검색하고, 이를 기반으로 LLM과의 통합을 성공적으로 수행합니다.
3. 문제 정의와 배경 (Problem Statement & Background)
문제 정의
- KGQA의 목표:
- 입력: 지식 그래프 G, 자연어 질문 q.
- 출력: 질문에 대한 정답 노드 .
- {a_q\} \subset G
- GNN을 활용해 KGQA를 노드 분류 문제로 정의:
- h(l)v=ψ(h(l−1)v,∑v′∈Nvω(q,r)⋅m(l)vv′)

RAG에서의 그래프 정보 활용
- 기존 RAG는 텍스트 기반 정보 검색 후 이를 LLM에 제공했습니다.
- GNN-RAG는 그래프 정보를 텍스트화하여 LLM에 제공:
- 이러한 접근법은 LLM이 KG의 구조적 정보를 자연스럽게 활용할 수 있도록 지원
Knowledge: Jamaica → language_spoken → English
Question: Which language do Jamaican people speak?
4. GNN-RAG 프레임워크 (GNN-RAG Framework)
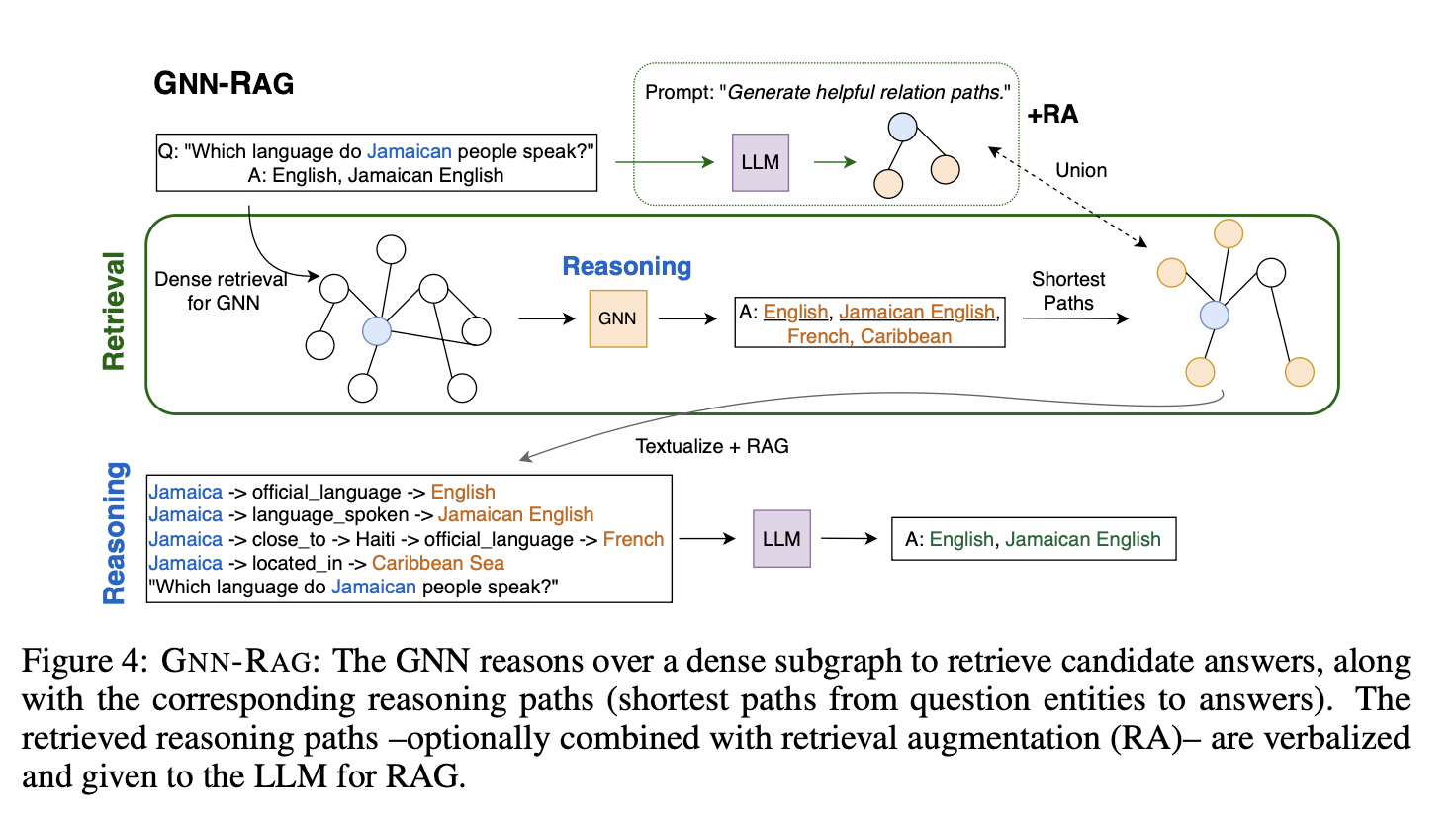
구성 요소
- GNN 학습:
- 질문에 따라 밀도 높은 하위 그래프에서 정답 후보를 추출하며, 학습 과정에서 최단 경로를 계산해 질문-정답 연결을 효율적으로 학습
- GNN은 각 노드를 정답 여부에 따라 분류하며, 다음의 손실 함수를 통해 최적화
- L=−∑v∈Gqyvlogpv

- LLM 통합:
- GNN이 생성한 정보를 텍스트화하여 LLM 입력으로 제공.
- 프롬프트 최적화:
- 이는 LLM이 효율적으로 정보를 이해하고 정확한 응답을 생성할 수 있도록 도움.
Based on the reasoning paths, please answer the given question.
Reasoning Paths: {Reasoning Paths}
Question: {Question}
4-1. Retrieval Augmentation (RA)
개념
- GNN 기반 검색과 LLM 기반 검색을 결합하여 성능을 강화.
- RA 경로:
- 이 방식은 GNN과 LLM의 상호 보완적 강점을 결합하여 정보 검색의 다양성과 정확도를 향상시킵니다.
- RA 경로=GNN 경로∪LLM 경로
효과
- 다중 홉 질문에서 GNN이 강점을 발휘하며, 복잡한 그래프 경로를 효과적으로 탐색.
- 단일 홉 질문에서는 LLM의 자연어 이해 능력을 활용하여 정답 검색 성능을 개선.
한계
- LLM 입력 길이가 길어질 경우 성능이 저하될 수 있으며, RA 경로의 최적화된 조합 방식이 요구됩니다.
5. 실험 결과 (Results)
주요 결과
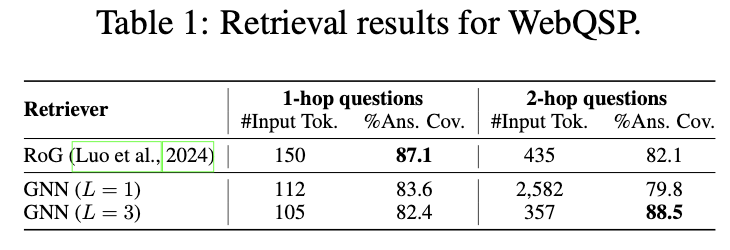
- WebQSP와 CWQ 데이터셋에서 최고 성능 기록.
- GNN-RAG+RA는 RoG 대비 Hit@10에서 WebQSP는 11.8%p, CWQ는 16.6%p 향상.
- F1 기준으로도 각각 2.2%p, 1.0%p 상승.
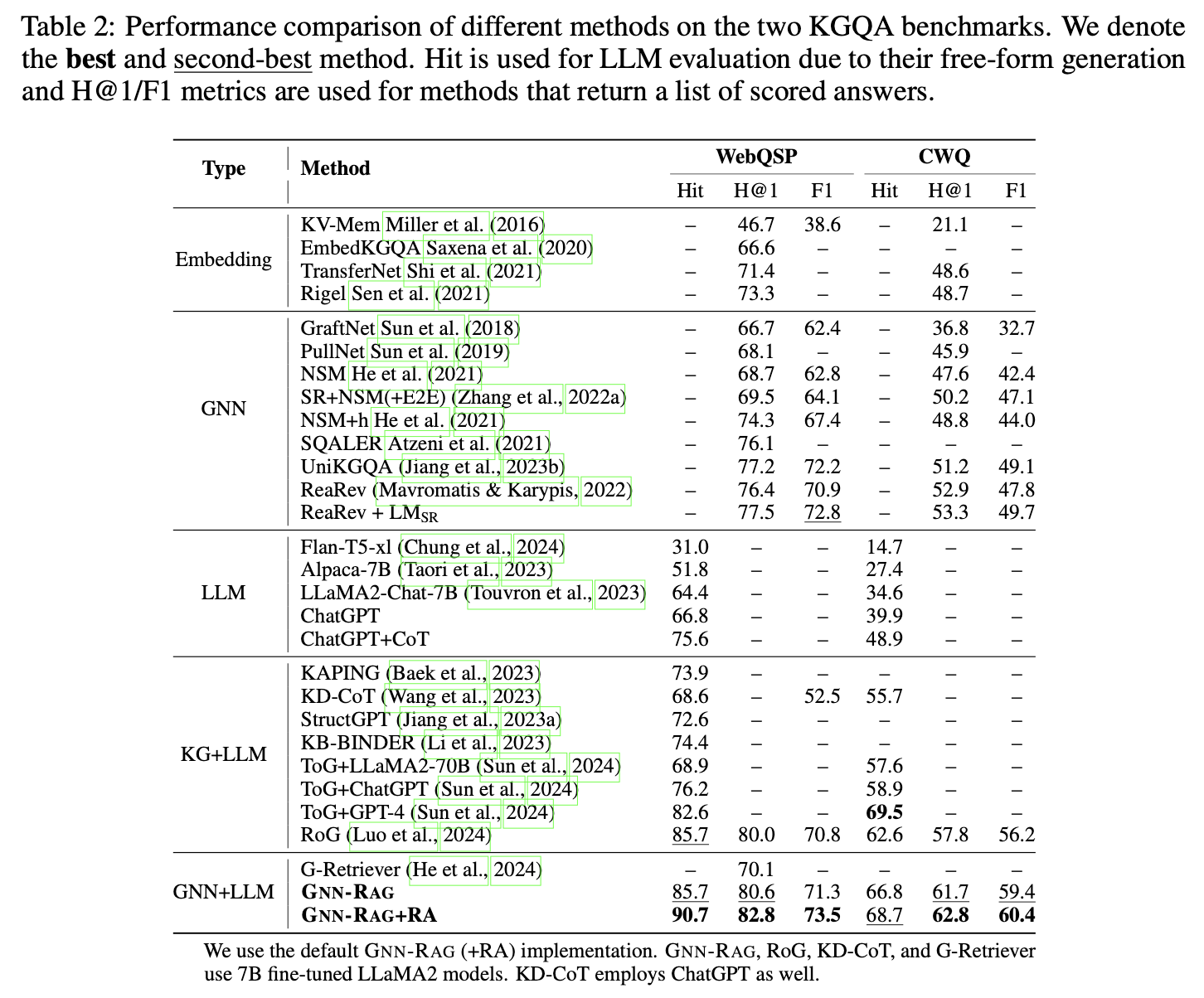
복잡한 질문에서의 성능
- WebQSP: 다중 홉 질문에서 RoG 대비 F1 7.8%p 향상.
- CWQ: 다중 엔터티 질문에서 7.3%p 향상.
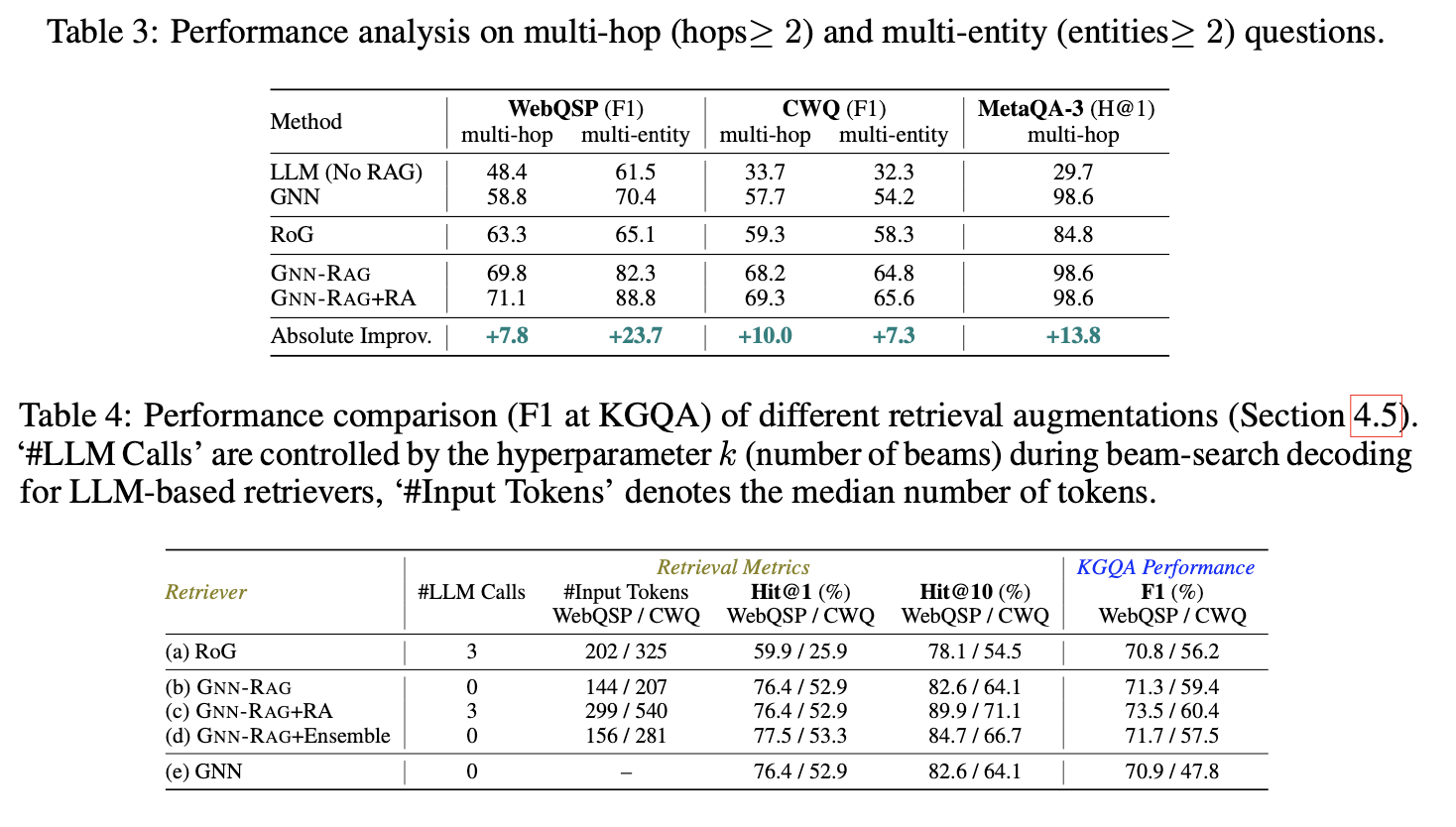
- GNN-RAG가 LLM의 신뢰성을 높인 2가지 케이스

- LLM(backbone)에 따른 성능 비교
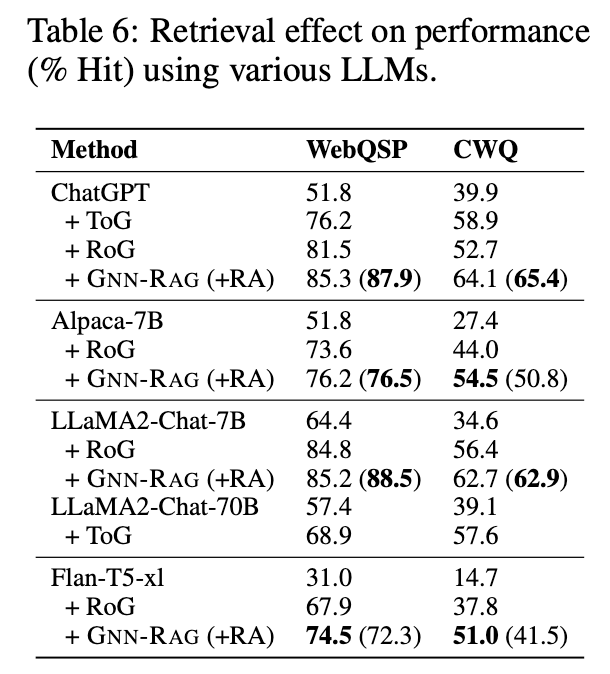
6. 결론 (Conclusion)
GNN-RAG는 GNN의 구조적 강점과 LLM의 자연어 이해 능력을 결합하여 KGQA 문제를 해결하는 데 효과적인 프레임워크입니다. 특히 Retrieval Augmentation(RA)를 통해 복잡한 질문에서도 높은 성능을 발휘하며, 효율성과 확장 가능성 면에서도 뛰어난 결과를 보여줍니다. 이 연구는 앞으로도 KGQA 연구 및 응용 분야에서 중요한 역할을 할 것으로 기대됩니다.
해당 논문은 Graph 접근만이 아닌 기존의 Text-RAG를 통합하여 제공하는 방법론입니다. 제안된 방법은 매우 간단해보이지만 이전 논문 리뷰를 했던 ToG와의 비교하여 더 높은 성능을 보였음을 입증했습니다. 최근 본 논문들은 iterative한 과정을 통해 추론적을 높이고자 했는데 이 논문에서의 방법은 보다 간단하면서 비용적 측면에서도 우수해 보입니다.
다음에는 여러 논문의 방법론을 비교해볼까 합니다.
'STUDY > Paper Review' 카테고리의 다른 글
| [Paper Review] Graphusion (0) | 2025.03.26 |
|---|---|
| [Paper Review] Think-on-Graph 2.0 (0) | 2025.03.02 |
| [Paper review] GraphRAG 논문 비교 (0) | 2025.02.22 |
| [Paper review] THINK-ON-GRAPH: DEEP AND RESPONSIBLE REASONING OF LARGE LANGUAGE MODEL ON KNOWLEDGE GRAPH (0) | 2025.01.21 |
| [Paper review] Don’t Do RAG:When Cache-Augmented Generation is All You Need for Knowledge Tasks (0) | 2025.01.08 |




