Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 마이온컴퍼니
- graphrag
- DP
- DFS
- 시각화
- 프로젝트
- GIS
- 인턴10
- GNN
- likelionlikelion
- intern10
- 멋쟁이사자처럼
- SQL
- ux·ui디자인
- 마이온
- Python
- folium
- paper review
- Rag
- parklab
- seaborn
- likelion
- Join
- 그리디
- TiL
- 멋사
- 멋재이사자처럼
- 알고리즘
- 파이썬
- BFS
Archives
- Today
- Total
지금은마라톤중
[GNN] Lecture 2_(2) : 전통 그래프 본문
이웃 중첩 검출
그래프 통계량
- 노드 및 그래프 분류 작업에 유용함
- 노드 간 관계를 정량화하지는 않음 - 관계 예측 문제에 적용하기 어려움
⇒ 이웃 중첩 검출
- 노드 쌍(pair) 사이의 관계성을 정량화하기 위해 이웃 중첩을 통계적으로 측정
- 노드-노드 유사도 행렬
- 가장 단순한 방법은 공통 이웃의 수를 세는 것
- 이웃 중첩 통계량은 관계 예측에 활용될 수 있음
- 노드-노드 유사성과 문턱(threshold) 값을 통해 관계 예측 가능

지역적 중첩 통계량
- 두 노드의 공통 이웃의 수를 활용한 함수를 적용하는 것이 일반적
- 노드 연결수에 의한 편향(bias)를 줄이기 위한 정규화 방법을 고안


- 각 공통 이웃의 중요도를 함께 고려하려는 방법도 활용됨
- 두 방법 모두 연결수가 작은 경우 더 높은 가중치를 주는 측정 방식

전역적 중첩 통계량
- 지역적 중첩 측정은 뛰어난 성능을 보이기도 하지만 지역적 이웃 관계만 고려한다는 한계 존재
- 지역적 중첩이 없더라도 같은 커뮤니티에 속할 수 있음 - 전역적 중첩을 평가하려는 시도

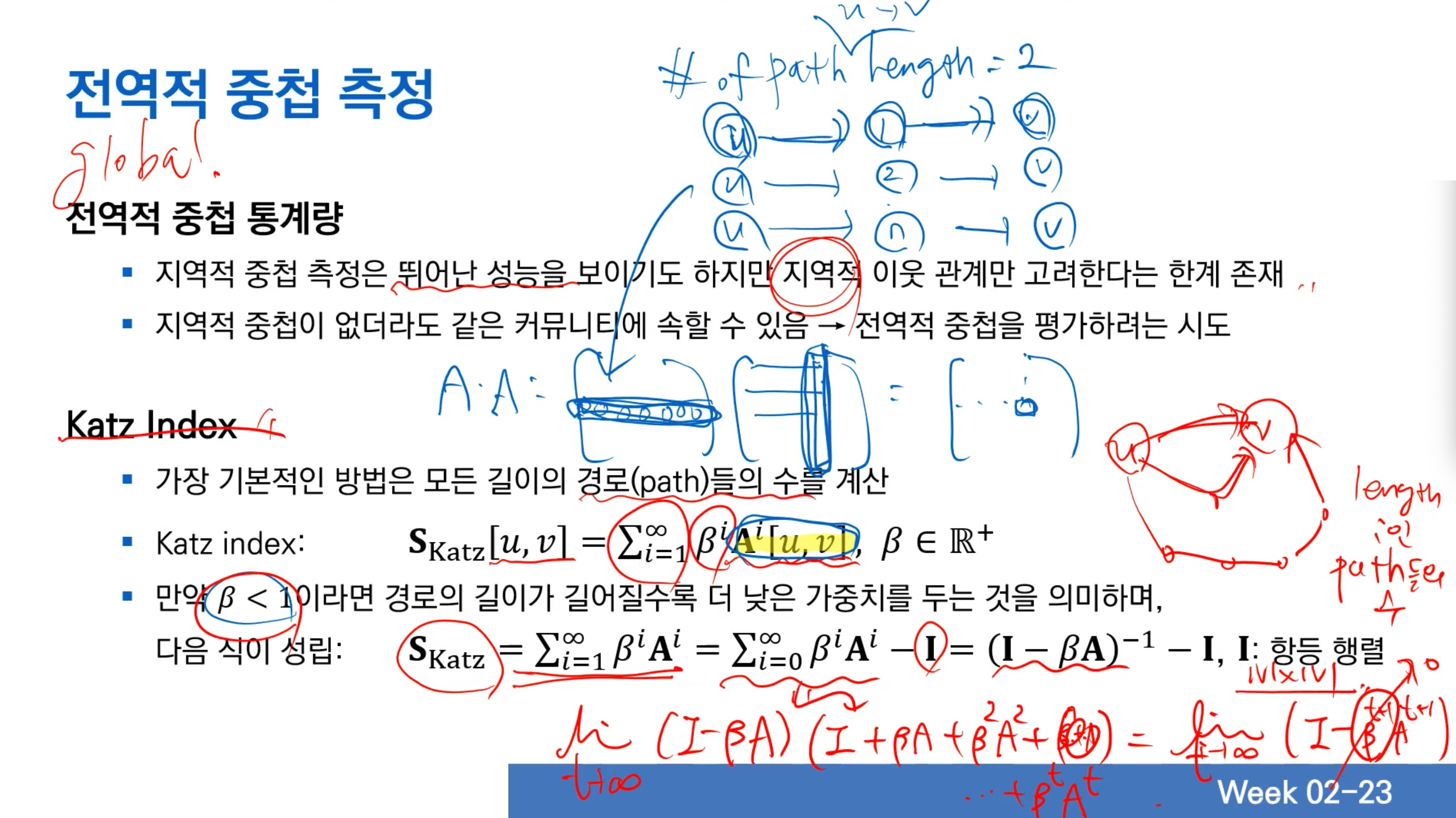
-
- Katz index는 노드 연결수가 큰 경우 높은 유사도가 높게 나오는 경향이 있음
- 이를 해결하기 위해 두 노드 사이의 경로 수의 기대값 대비 실제 수를 고려:
- 무작위 그래프의 일반화인 configuration model을 활용하여 계산
- degree를 고려한 노드 사이의 연결이 있을 확률을 고려함.

- 하지만 경로의 길이가 3 이상인 경우 정확한 값을 계산하기 상당히 어려움LHN Similarity


- → 전역적인 중첩 측정 방법
- 경로의 수를 직접 세는 대신 무작위 행보를 활용할 수 있음
- 예를 들면, PageRank의 변형인 Personalized PageRank 알고리즘 활용 가능
- 한 노드에서 다른 노드로 도달하는 정도(likelihood)의 합으로 유사도 정의
- 𝐏 = 𝐀𝐃^−1 : 전이 확률(transition probability)을 표현한 확률 행렬(stochastic matrix)
- e_𝑢: 노드 𝑢의 위치만 1이고 나머지는 0인 벡터
- 1 − 𝑐: 재시작(restart) 확률, 𝑐: damping factor무작위 행보 방법

그래프 라플라시안
- 노드 군집화
- 앞선 절은 그래프 데이터의 분류, 관계 예측에 대한 전통적인 방법들을 다룸
- 이번 절은 군집화를 위한 노드의 저차원 임베딩, 행렬과 그래프 이론의 기초에 대해 소개함
- 그래프 라플라시안
- 인접 행렬: 정보 손실 없이 그래프를 표현 가능
- 다른 행렬 표현: 유용한 수학적 성질을 가지는 대체 행렬 표현이 존재
- 그래프 라플라시안: L= D- A
- 정규화된 그래프 라플라시안:


그래프 라플라시안
- 그래프 내에서 최적의 노드 군집화를 제공하는데 활용 가능
- 그래프 컷 최소화 문제와 밀접한 관계


- 컷 최소화 문제를 개선하는 아래와 같은 방법들이 존재
- Ratio Cut: 적은 수의 노드를 지닌 군집에 페널티 부여
- Normalized Cut (NCut): 적은 수의 링크를 지닌 군집에 페널티 부여




스펙트럴 군집화



출처 :
- William L. Hamilton. (2020). Graph Representation Learning.
- 충남대학교 임성수 교수님 그래프 기계학습 강의
'GNN' 카테고리의 다른 글
| [GNN] 노드분류와 링크예측 실습(feat.DGL) (0) | 2024.11.29 |
|---|---|
| [GNN] Networkx 실습 (1) | 2024.11.14 |
| [GNN] Lecture 2 _(1) : 전통 그래프 (1) | 2024.09.29 |
| [GNN] Lecture 1 : 그래프 소개 (0) | 2024.09.29 |
| [GNN] Overview (2) | 2024.09.28 |
Comments





